Ten annotated online resources
I used the following 4 questions to guide a more thorough evaluation of some of the 20 online resources in this resource library. See detailed answers below several of the resources listed.
- What is being learned? What are the underlying assumptions (explicit and implicit) about the nature of knowledge?
- How does learning take place? What are the underlying assumptions (explicit or implicit) about the nature of learning
- What role does technology play? What advantages or disadvantages does the technology hold for this role? What unique contribution does the technology make in facilitating learning?
- How does it fit within existing school curriculum? (e.g., is it intended to supplement or supplant existing curriculum? Is it intended to enhance the learning of something already central to the curriculum or some new set of understandings or competencies?)
#3 Barbie Bungee
|
The consideration of cord length is very important in a bungee jump—too short, and the jumper doesn’t get much of a thrill; too long, and ouch! In this lesson, students model a bungee jump using a Barbie® doll and rubber bands. The distance to which the doll will fall is directly proportional to the number of rubber bands, so this context is used to examine linear functions.
|
|
The rules of Krypto are amazingly simple — combine five numbers using the standard arithmetic operations to create a target number. Finding a solution to one of the more than 3 million possible combinations can be quite a challenge, but students love it. And you’ll love that the game helps to develop number sense, computational skill, and an understanding of the order of operations.
|
#4 Exploring Krypto
|
This activity is designed based on a popular card game where students use a series of 5 number cards and basic arithmetic operations to compute a target number. Students will be practices their basic computational skills with integers and learning how to use arithmetic operations and grouping symbols. It assumes that learning can take place through exploration, trial and error, and construction of knowledge via scaffolding.
Learning takes place through trial and error and teacher-to-peer and peer-to-peer interactions. Students can draw on their interactions with others and build their mathematical vocabulary and they begin to explain computations. It can also serve as a bridge to discussing the properties of real numbers such as associative, commutative, distributive, etc.
In this activity, the technology is a bit more limiting than the actual card game because it restricts the integers used to values from 1 to 10. Also, the structure of the website automatically embeds the numbers in a way that imposes certain operations. On the up side, students can build their skills slowly by using the hints, seeing a solution instantly if they are stuck and then re-setting. Also, if students are in a computer lab, everyone can play and learn from the experience if a deck of cards isn’t available for all students.
Order of operations and properties of real numbers is a part of the current curriculum. NCTM also stresses the importance of students being able to understand numbers, ways of representing numbers, relationships among numbers, and number systems.
Learning takes place through trial and error and teacher-to-peer and peer-to-peer interactions. Students can draw on their interactions with others and build their mathematical vocabulary and they begin to explain computations. It can also serve as a bridge to discussing the properties of real numbers such as associative, commutative, distributive, etc.
In this activity, the technology is a bit more limiting than the actual card game because it restricts the integers used to values from 1 to 10. Also, the structure of the website automatically embeds the numbers in a way that imposes certain operations. On the up side, students can build their skills slowly by using the hints, seeing a solution instantly if they are stuck and then re-setting. Also, if students are in a computer lab, everyone can play and learn from the experience if a deck of cards isn’t available for all students.
Order of operations and properties of real numbers is a part of the current curriculum. NCTM also stresses the importance of students being able to understand numbers, ways of representing numbers, relationships among numbers, and number systems.
#5 Create a Graph
|
Graphs and charts are great because they communicate information
visually. For this reason, graphs are often used in newspapers,
magazines and businesses around the world.
Graphs or charts can help impress people by getting your point across quickly and visually. This activity allows students to choose from 5 different types of graphs and use their data to create graphs that best effectively communicate the information collected. |
This resource is a tool for representing data with a variety of different graphs. There is no specific mathematical skill or concept being learned with this technological tool. Although not in the NCTM Algebra strand, we often analyze and represent data collected in the Algebra course as we prepare students for mathematical modeling of linear, quadratic, exponential, and other functions. NCTM states that it is important for students to select and use appropriate statistical methods to analyze data. Students will learn about the various representations, which are good for univariate data and which may be for bivariate or other types. They will also have to make decisions about what formats best communicate the trend of the data in a meaningful way.
The technology allows for more class time to be used analyzing the data in a larger context and not using paper/pencil methods for graphing. Students are able to handle and represent larger data sets enhancing the quality of their investigation.
It is important that students learn to represent data in a variety of ways. This is a concept/skill that has been weaved into the curriculum every year and the use of this tool would be a great intermediate step for data representation allowing students to easily transition into the use of spreadsheets and other more sophisticated tools.
The technology allows for more class time to be used analyzing the data in a larger context and not using paper/pencil methods for graphing. Students are able to handle and represent larger data sets enhancing the quality of their investigation.
It is important that students learn to represent data in a variety of ways. This is a concept/skill that has been weaved into the curriculum every year and the use of this tool would be a great intermediate step for data representation allowing students to easily transition into the use of spreadsheets and other more sophisticated tools.
In this lesson, students have the opportunity to learn about various representations of a trinomial and make the connections between standard form, factored form, and also explore visual representations and the connection to area. With the use of a carefully crafted lesson, students can use this interactive to learn to factor trinomials.
This learning takes place by allowing students to explore and use their prior knowledge and conceptual understanding of rectangular area and finding the product of binomials.
This activity and mode of exploration allows students to represent ideas in new and different ways. It also aligns with the NCTM Algebra standard calling for students to represent and analyze mathematical situations and structures using algebraic symbols.
This is a topic addressed in the current curriculum that students tend to struggle with. If they master the skill, much of the time it is only mechanically, but students lack a deeper understanding of the concept. Use of this activity may help bridge some of the gaps and facilitate a deeper understanding.
This learning takes place by allowing students to explore and use their prior knowledge and conceptual understanding of rectangular area and finding the product of binomials.
This activity and mode of exploration allows students to represent ideas in new and different ways. It also aligns with the NCTM Algebra standard calling for students to represent and analyze mathematical situations and structures using algebraic symbols.
This is a topic addressed in the current curriculum that students tend to struggle with. If they master the skill, much of the time it is only mechanically, but students lack a deeper understanding of the concept. Use of this activity may help bridge some of the gaps and facilitate a deeper understanding.
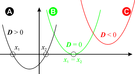
This investigation allows students to explore the connections between the coefficients of a quadratic equation and the solutions, discriminant, and the x-intercepts graph of the function. It is designed in such a way that assumes learning and understanding is constructed through observation and manipulation. As a by-product, students may also learn more about the structure of the graph of a quadratic including the vertex, symmetry, y-intercept, whether it has a minimum or a maximum, etc.
The learning takes place primarily through exploration and can be made more dynamic if structured correctly by a facilitator. NCTM stresses the importance of students being able to represent and analyze mathematical situations and structures using algebraic symbols. This activity will definitely help develop these skills in students.
Every topic introduced here in a part of the traditional Algebra 1 curriculum. However, so many more extensions can built as students investigate the path that vertices make when changing the b-value. Students could also use the applet to model situations with a quadratic. Here, the possibilities seem endless.
The learning takes place primarily through exploration and can be made more dynamic if structured correctly by a facilitator. NCTM stresses the importance of students being able to represent and analyze mathematical situations and structures using algebraic symbols. This activity will definitely help develop these skills in students.
Every topic introduced here in a part of the traditional Algebra 1 curriculum. However, so many more extensions can built as students investigate the path that vertices make when changing the b-value. Students could also use the applet to model situations with a quadratic. Here, the possibilities seem endless.
|
The screen in this applet is designed to help students visualize the principal trigonometric functions sin, cos and tan. It also allows for the exploration of their inverse functions, their reciprocal functions and square functions. Relationships between these functions can be investigated. Identities such as cos²x + sin²x = 1 become clear.
|
#10 Comparing graphs of Trigonometric Functions
|
This is one of my favorite activities more because I am a math geek than for its educational value. This is another educational tool that should be used in the context of a larger lesson developed by a thoughtful instructor. The applet quickly graphs a variety of trigonometric functions all on the same axis and the analysis of the graphs can help make the connections between the trigonometric functions come alive.
Learning takes place here by providing students with the opportunity to visually represent concepts that have been studied for trigonometric functions and their inverses. It is assumed here that students understand where the values for the trigonometric functions are derived from as it does not make any connections to the unit circle. Also, this tool assumes familiarity with radians as the axis is labeled accordingly.
The Algebra 2 curriculum includes a variety of trigonometry topics. This tool does not address either of the topics, per se, but it does allow for a deeper investigation and connections to be made about the trigonometry topics that are covered with the students.
Learning takes place here by providing students with the opportunity to visually represent concepts that have been studied for trigonometric functions and their inverses. It is assumed here that students understand where the values for the trigonometric functions are derived from as it does not make any connections to the unit circle. Also, this tool assumes familiarity with radians as the axis is labeled accordingly.
The Algebra 2 curriculum includes a variety of trigonometry topics. This tool does not address either of the topics, per se, but it does allow for a deeper investigation and connections to be made about the trigonometry topics that are covered with the students.